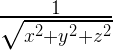алгоритмы и алгоритмические трюки
Модератор: Olej
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
 алгоритмы и алгоритмические трюки
алгоритмы и алгоритмические трюки
Есть такие не очевидные трюки, которые позволяют иногда на порядок ускорить вычисление результата.
Обычно, они (такие трюки) относятся к очень часто используемых вычислений.
Профессиональному программисту нужно бы такие вычисления-трюки знать наперёд.
Поэтому для их фиксации - вот такая отдельная тема.
Отдельная тема ещё потому, что такие трюки не зависят от языка программирования, могут использоваться везде ... и было бы неразумно включать их в существующие темы форума, посвящённые конкретным языкам программирования.
Обычно, они (такие трюки) относятся к очень часто используемых вычислений.
Профессиональному программисту нужно бы такие вычисления-трюки знать наперёд.
Поэтому для их фиксации - вот такая отдельная тема.
Отдельная тема ещё потому, что такие трюки не зависят от языка программирования, могут использоваться везде ... и было бы неразумно включать их в существующие темы форума, посвящённые конкретным языкам программирования.
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
Re: алгоритмические трюки
«Магическая константа» 0x5f3759dfOlej писал(а):Есть такие не очевидные трюки, которые позволяют иногда на порядок ускорить вычисление результата.
Обычно, они (такие трюки) относятся к очень часто используемых вычислений.
Зачем?:В этой статье мы поговорим о «магической» константе 0x5f3759df, лежащей в основе элегантного алгоритмического трюка для быстрого вычисления обратного квадратного корня.
Вот полная реализация этого алгоритма:Код: Выделить всё
float FastInvSqrt(float x) { float xhalf = 0.5f * x; int i = *(int*)&x; // представим биты float в виде целого числа i = 0x5f3759df - (i >> 1); // какого черта здесь происходит ? x = *(float*)&i; x = x*(1.5f-(xhalf*x*x)); return x; }
А то, почему такой "дикий" код, смешивающий int и float представления, работает - подробно анализируется в статье.Зачем вообще нам может понадобиться считать обратный квадратный корень, да ещё и пытаться делать это настолько быстро, что нужно реализовывать для этого специальные хаки? Потому, что это одна из основных операций в 3D программировании. При работе с 3D графикой используются нормали поверхностей. Это вектор (с тремя координатами) длиной в единицу, который нужен для описания освещения, отражения и т.д. Таких векторов нужно много. Нет, даже не просто много, а МНОГО. Как мы нормализуем (приводим длину к единице) вектор? Мы делим каждую координату на текущую длину вектора. Ну или, перефразируя, умножаем каждую координату вектора на величину:
Расчёт image относительно прост и работает быстро на всех типах процессоров. А вот расчёт квадратного корня и деление – дорогие операции. И вот поэтому – встречайте алгоритм быстрого извлечения обратного квадратного корня — FastInvSqrt.
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
Re: алгоритмические трюки
Ещё один очень частый случай:
- В обработке временных рядов, цифровой обработке сигналов и для других целей часто вычисляется среднее и дисперсия (и, далее, среднеквадратичное отклонение) числовой последовательности X[ i ]: mean = 1 / N * ∑( X[ i ] ), disp = 1 / N * ∑( ( X[ i ] - mean )^2 ). Но прямое вычисление характеристик по математическим формулам требует 2-х проходов: сначала вычисление среднего, а затем уже — дисперсии.
- В этом есть много минусов: в 2 раза больше перебор, промахи попаданий в кэш при повторном проходе ... но самое худшее при этом то, что нужно хранить в памяти задачи всю последовательность чисел, что при больших N, например, 10M double ... или просто непрерывный поток входных отсчётов, неприемлемо.
Т.е. такое вычисление "в лоб", из учебника, выглядит примерно как-то так:
Здесь: s1 - среднее, постоянная составляющая сигнала, s2 - дисперсия, мера разброса, отклонения от среднего, мощность сигнала.
Если раскрыть выражение (квадрат разности) для дисперсии и произвести дальнейшие упрощения, то можно прийти к выражению: disp = 1 / N * ∑( X[ i ] 2 ) - mean2. Теперь мы можем накапливать сумму квадратов последовательности чисел в потоке, а вычисление характеристик отложить на завершение:
Если же вам нужно СКО, линейное среднеквадратичное отклонение ряда, то оно:
- В обработке временных рядов, цифровой обработке сигналов и для других целей часто вычисляется среднее и дисперсия (и, далее, среднеквадратичное отклонение) числовой последовательности X[ i ]: mean = 1 / N * ∑( X[ i ] ), disp = 1 / N * ∑( ( X[ i ] - mean )^2 ). Но прямое вычисление характеристик по математическим формулам требует 2-х проходов: сначала вычисление среднего, а затем уже — дисперсии.
- В этом есть много минусов: в 2 раза больше перебор, промахи попаданий в кэш при повторном проходе ... но самое худшее при этом то, что нужно хранить в памяти задачи всю последовательность чисел, что при больших N, например, 10M double ... или просто непрерывный поток входных отсчётов, неприемлемо.
Т.е. такое вычисление "в лоб", из учебника, выглядит примерно как-то так:
Код: Выделить всё
#define n 1000000
double x[ n ], s1 = 0.0, s2 = 0.0;
for( int i = 0; i < n; i++ )
s1 += x[ i ];
s1 /= n;
for( int i = 0; i < n; i++ )
s2 += ( x[ i ] - s1 ) * ( x[ i ] - s1 );
s2 = s2 / n
Если раскрыть выражение (квадрат разности) для дисперсии и произвести дальнейшие упрощения, то можно прийти к выражению: disp = 1 / N * ∑( X[ i ] 2 ) - mean2. Теперь мы можем накапливать сумму квадратов последовательности чисел в потоке, а вычисление характеристик отложить на завершение:
Код: Выделить всё
#define n 1000000
double x[ n ], s1 = 0.0, s2 = 0.0;
for( int i = 0; i < n; i++ ) {
s1 += d;
s2 += d * d;
}
s1 /= n;
s2 = s2 / n - s1 * s1;
Код: Выделить всё
s2 = sqr( s2 );
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
Re: алгоритмические трюки
Olej писал(а):А то, почему такой "дикий" код, смешивающий int и float представления, работает - подробно анализируется в статье.
Код: Выделить всё
#include <stdio.h>
#include <math.h>
float FastInvSqrt( float x ) {
float xhalf = 0.5f * x;
int i = *(int*)&x; // представим биты float в виде целого числа
i = 0x5f3759df - ( i >> 1 ); // какого черта здесь происходит ?
x = *(float*)&i;
x = x * ( 1.5f - ( xhalf * x * x ) ); // одна итерация уточнения (метод Ньютона)
return x;
}
int main( void ) {
float x[] = { .1, 1., 20, 50, 100, 200 };
for( int i = 0; i < sizeof( x ) / sizeof( *x ); i++ ) {
float s1 = 1. / sqrt( x[ i ] ), s2 = FastInvSqrt( x[ i ] );
printf( "%8.2f:\t%f\t%f\t[%f%]\n", x[ i ], s1, s2, ( s1 / s2 - 1. ) * 100 );
}
return 0;
}
Код: Выделить всё
[olej@dell sqrt]$ gcc -lm fsqrti.c -o fsqrti
[olej@dell sqrt]$ ./fsqrti
0.10: 3.162278 3.157232 [0.159812%]
1.00: 1.000000 0.998307 [0.169575%]
20.00: 0.223607 0.223571 [0.016224%]
50.00: 0.141421 0.141356 [0.046277%]
100.00: 0.100000 0.099845 [0.155365%]
200.00: 0.070711 0.070678 [0.046277%]
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
Re: алгоритмические трюки
По мотивам этой статьи можно построить и вычисление корня квадратного (без инверсии, 1/sqrt()):Olej писал(а):А то, почему такой "дикий" код, смешивающий int и float представления, работает - подробно анализируется в статье.
Код: Выделить всё
#include <stdio.h>
#include <math.h>
float FastInvSqrt( float x ) {
int i = *(int*)&x; // представим биты float в виде целого числа
i = 0x1fbd1df5 + ( i >> 1 );
float y = *(float*)&i;
y = y - ( y * y - x ) / 2. / y; // одна итерация уточнения (метод Ньютона)
return y;
}
int main( void ) {
float x[] = { .1, 1., 20, 50, 100, 200 };
for( int i = 0; i < sizeof( x ) / sizeof( *x ); i++ ) {
float s1 = sqrt( x[ i ] ), s2 = FastInvSqrt( x[ i ] );
printf( "%8.2f:\t%f\t%f\t[%f%]\n", x[ i ], s1, s2, ( s1 / s2 - 1. ) * 100 );
}
return 0;
}
Код: Выделить всё
[olej@dell sqrt]$ gcc -lm fsqrt.c -o fsqrt
[olej@dell sqrt]$ ./fsqrt
0.10: 0.316228 0.316243 [-0.004882%]
1.00: 1.000000 1.000064 [-0.006413%]
20.00: 4.472136 4.472575 [-0.009817%]
50.00: 7.071068 7.071161 [-0.001317%]
100.00: 10.000000 10.000242 [-0.002420%]
200.00: 14.142136 14.142322 [-0.001317%]
Код: Выделить всё
y = y - ( y * y - x ) / 2. / y; // одна итерация уточнения (метод Ньютона)
Код: Выделить всё
[olej@dell sqrt]$ ./fsqrt
0.10: 0.316228 0.319369 [-0.983626%]
1.00: 1.000000 0.988738 [1.138985%]
20.00: 4.472136 4.409907 [1.411116%]
50.00: 7.071068 7.034907 [0.514019%]
100.00: 10.000000 10.069814 [-0.693297%]
200.00: 14.142136 14.069814 [0.514019%]
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
Re: алгоритмические трюки
Аналогично можно извлекать и корень кубический (степень 0.333):Olej писал(а): По мотивам этой статьи можно построить и вычисление корня квадратного (без инверсии, 1/sqrt()):
Код: Выделить всё
#include <stdio.h>
#include <math.h>
float FastInvSqrt( float x ) {
int i = *(int*)&x; // представим биты float в виде целого числа
i = (int)( 0x2a517d3c + ( 0.333f * i ) );
x = *(float*)&i;
return x;
}
int main( void ) {
float x[] = { .1, 1., 20, 50, 100, 200 };
for( int i = 0; i < sizeof( x ) / sizeof( *x ); i++ ) {
float s1 = powf( x[ i ], 0.333f ),
s2 = FastInvSqrt( x[ i ] );
printf( "%8.2f:\t%f\t%f\t[%f%]\n", x[ i ], s1, s2, ( s1 / s2 - 1. ) * 100 );
}
return 0;
}
Код: Выделить всё
[olej@dell sqrt]$ gcc -lm fsqrt3.c -o fsqrt3
[olej@dell sqrt]$ ./fsqrt3
0.10: 0.464515 0.448858 [3.488183%]
1.00: 1.000000 0.963818 [3.754067%]
20.00: 2.711709 2.685760 [0.966132%]
50.00: 3.679231 3.559906 [3.351903%]
100.00: 4.634469 4.451782 [4.103673%]
200.00: 5.837716 5.783813 [0.931954%]
Можете это доделать сами ... метод Ньютона описан здесь.
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
Re: алгоритмические трюки
В комментариях публикации обстоятельно обсуждается, что это всё работает, если компилятору С/C++ установлена опция -no-strict-aliasing (или по умолчанию установлено). Или на другой аппаратной платформе, отличной от x86.Olej писал(а):А то, почему такой "дикий" код, смешивающий int и float представления, работает - подробно анализируется в статье.
Это достаточно интересно...
Но у GCC нет этой опции:
Код: Выделить всё
[olej@dell sqrt]$ gcc -no-strict-aliasing -lm fsqrt.c -o fsqrt
gcc: ошибка: unrecognized command line option «-no-strict-aliasing»
Скорее всего, обсуждение касается LLVM.
Подробно разъяснения по опции см. По следам C++ Siberia: дракон в мешке.
В конце концов ... если есть опасения, проблема решается (один из способов) так:
Код: Выделить всё
#include <stdio.h>
#include <math.h>
#include <string.h>
float FastInvSqrt( float x ) {
int i;
memcpy( &i, &x, sizeof( float ) ); // представим биты float в виде целого числа
i = 0x1fbd1df5 + ( i >> 1 );
float y;
memcpy( &y, &i, sizeof( float ) );
y = y - ( y * y - x ) / 2. / y; // одна итерация уточнения (метод Ньютона)
return y;
}
int main( void ) {
float x[] = { .1, 1., 20, 50, 100, 200 };
for( int i = 0; i < sizeof( x ) / sizeof( *x ); i++ ) {
float s1 = sqrt( x[ i ] ), s2 = FastInvSqrt( x[ i ] );
printf( "%8.2f:\t%f\t%f\t[%f%]\n", x[ i ], s1, s2, ( s1 / s2 - 1. ) * 100 );
}
return 0;
}
Код: Выделить всё
[olej@dell sqrt]$ gcc -lm fsqrtc.c -o fsqrtc
[olej@dell sqrt]$ ./fsqrtc
0.10: 0.316228 0.316243 [-0.004882%]
1.00: 1.000000 1.000064 [-0.006413%]
20.00: 4.472136 4.472575 [-0.009817%]
50.00: 7.071068 7.071161 [-0.001317%]
100.00: 10.000000 10.000242 [-0.002420%]
200.00: 14.142136 14.142322 [-0.001317%]
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
Re: суффиксные деревья и поиск в строке
Книга в порядке справочника по алгоритмам:

Скачивайте (PDF) здесь.
Хотя эта книга и задумана как учебник...

Скачивайте (PDF) здесь.
Такие справочники сильно бывают нужны на этапе начального выбора алгоритма для практической задачи.Дж. Макконнелл
Основы современных алгоритмов. 2-едополненное издание Москва:
Техносфера, 2004. - 368с.
ISBN 5-94836-005-9
Хотя эта книга и задумана как учебник...
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
Re: суффиксные деревья и поиск в строке
Ещё одна книга-справочник по алгоритмам.Olej писал(а):Книга в порядке справочника по алгоритмам:
Качаем здесь: Алгоритмы C++.pdf.e-maxx ::algo
Вас приветствует книга, собранная по материалам сайта e-maxx.ru/algo (по состоянию на 20 Sep 2010 18:56).
В этой книге Вы найдёте описание, реализации и доказательства множества алгоритмов, от известных всем до
тех, которые являются уделом лучших олимпиадников и специалистов по Computer Science. В конце приведены ссылки на тематическую литературу, которую можно скачать с моего сайта, а также немного информации обо мне.
Приятного чтения!
- Olej
- Писатель
- Сообщения: 21338
- Зарегистрирован: 24 сен 2011, 14:22
- Откуда: Харьков
- Контактная информация:
Re: алгоритмы и алгоритмические трюки
Жадные алгоритмы - вполне заслуживают отдельного упоминания как целый класс алгоритмов... как вариант решения вашей задачи.Olej писал(а):Есть такие не очевидные трюки, которые позволяют иногда на порядок ускорить вычисление результата.
Жадный алгоритм:
Переводя с языка математического на человеческий, это выглядит так:Жадный алгоритм (англ. Greedy algorithm) — алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным.
- когда есть возможность выбора N разных вариантов, то на каждом шаге выбираем вариант, с наилучшим результатом на этом шаге...
- то же самое повторяем для оставшихся N-1 возможных выборов...
- и так повторяем до тех пор, пока варианты выбора исчерпаются, когда найдено искомое решение.
Вариант жадных алгоритмов требует обязательного упоминания по 2-м противоположным причинам:
1. Жадные алгоритмы, в некоторых случаях, позволяют сократить объём вычислений (вычислительную сложность) на много порядков ... по сравнению, например, с полным рекурсивным перебором вариантов.
2. Жадные алгоритмы, используя локальные оптимумы на каждом шаге, не для всяких задач позволяют найти глобальное оптимальное решение - примером таких не решаемых задач является общеизвестная задача о паковании оптимального рюкзака.
Анализ того, что для конкретной задачи жадный алгоритм даст глобальный оптимум, оставим для самостоятельного разбора любопытным:
Известно, что если структура задачи задается матроидом, тогда применение жадного алгоритма выдаст глобальный оптимум.
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей и 16 гостей